Equivalencias notables
- Todo número entero
 se puede escribir como fracción
se puede escribir como fracción 
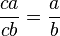 con
con  y
y 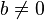
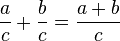

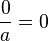 con
con 
 con
con  .
.
Propiedades
- El conjunto
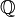 , con las propiedades de adición y multiplicación definidas más arriba, conforma un cuerpo conmutativo: el cuerpo de cocientes de los enteros
, con las propiedades de adición y multiplicación definidas más arriba, conforma un cuerpo conmutativo: el cuerpo de cocientes de los enteros 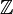 .
. - Los racionales son el menor cuerpo con característica nula.
- La clausura algebraica de
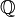 , es el conjunto de los números algebraicos.
, es el conjunto de los números algebraicos. - El conjunto de los números racionales es numerable, es decir que existe una biyección entre
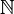 y
y 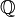 (tienen la misma cantidad de elementos). El conjunto de los número reales no es numerable (la parte no-denombrable de los reales, la constituyen los números irracionales).
(tienen la misma cantidad de elementos). El conjunto de los número reales no es numerable (la parte no-denombrable de los reales, la constituyen los números irracionales). - Propiedad arquimediana: el conjunto
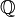 es denso en
es denso en  por construcción misma de
por construcción misma de  ; es decir, para cualquier pareja de números reales existe otro número racional situado entre ellos.
; es decir, para cualquier pareja de números reales existe otro número racional situado entre ellos. - Los racionales forman un dominio de factorización única ya que todo racional diferente de cero puede descomponerse en la forma:
 donde
donde  son números enteros primos,
son números enteros primos,  (siendo algunos de ellos negativos si q no es entero) y
(siendo algunos de ellos negativos si q no es entero) y  . Por ejemplo
. Por ejemplo  .
.
http://es.wikipedia.org/wiki/N%C3%BAmero_racional
No hay comentarios.:
Publicar un comentario